Защита программ с помощью сетей Петри — Архив WASM.RU
Когда сны становятся реальностью…
Что такое сеть Петри? Сеть Петри – это двудольный ориентированный мультиграф. Ну вот, я уже вижу, как большинство читателей в ужасе пытаются закрыть страницу. Но не стоит так пугаться - прочитайте спокойно до конца и, по крайней мере, вы узнаете кое-что новое и интересное.
Не бойтесь сетей Петри – за вычурным определением скрывается простейший, интуитивно понятный даже ребенку механизм. Для начала определим основные понятия из теории, без которых, к сожалению, дальнейшее продвижение просто невозможно: сеть Петри состоит из четырех элементов: множество позиций
(схематически обозначаются кружками), множества переходов
(обозначаются черточками), входной функции
и выходной функции
. Входная и выходная функции связаны с переходами и позициями. Входная функция
отображает переход
в множество позиций
, называемых входными позициями перехода. Выходная функция
отображает переход
в множество позиций
, называемых выходными позициями перехода. Ориентированные дуги (стрелки) соединяют позиции и переходы, при этом некоторые дуги направлены от позиций к переходам, а другие – от переходов к позициям.
Маркировка
- присвоение фишек позициям сети Петри. Фишка – примитивное понятие сетей Петри. Фишки используются для определения выполнения сети Петри.
Выполнением сети Петри управляют количество и распределение фишек в сети. Фишки находятся в кружках (позициях) и управляют выполнением переходов сети. Сеть Петри выполняется посредством запуска переходов. Переход может запускаться только в том случае, когда он разрешен.
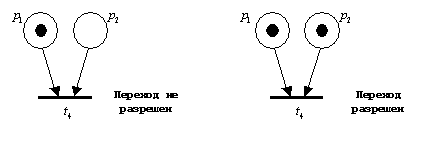
Переход называется разрешенным, если каждая из его входных позиций имеет число фишек по крайней мере равное числу дуг из позиции в переход. Прочитайте предыдущее предложение еще пару раз. Например, если позиции
и
служат входами для перехода
, тогда
разрешен, если
и
имеют хотя бы по одной фишке:
Для перехода
с входным комплектом
позиция
должна обладать по крайней мере тремя фишками, для того чтобы
был разрешен:

Переход запускается удалением всех разрешающих фишек из его входных позиций и последующим помещением в каждую из его выходных позиций, по одной фишке для каждой дуги. Из приведенных ниже графических иллюстраций все сразу станет понятно:
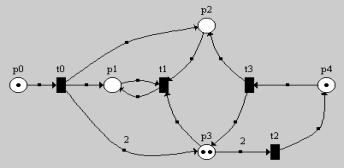
1
В данной сети переходы t0, t2 и t3 разрешены.
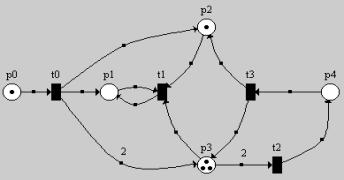
2
Маркировка, полученная в результате запуска перехода t3.
3
Маркировка, полученная в результате запуска перехода t0.
(обратите внимание - из t0 в p3 идет ДВЕ дуги!!! Поэтому в p3 добавилось ДВЕ фишки).
4
Маркировка, полученная в результате запуска перехода t2 (и снова обратите внимание на ДВЕ дуги, идущие из p3 в t2).
Всю эту игру можно продолжать до тех пор, пока хотя бы один из переходов будет разрешен. Поиск тупиковых ситуаций (когда ни один из переходов не является разрешенным) – тема отдельной статьи.
Теперь вы в самом первом приближении познакомились с сетью Петри, возможно, она напомнила давно забытую детскую игру…
Но довольно теории, полученных знаний вполне достаточно чтобы двигать дальше. За более глубоким погружением в удивительный мир сетей Петри обращайтесь к книге JamesL. Peterson-а, “Petrinettheoryandthemodelingofsystems”.
Теперь возникает резонный вопрос: как все это прикрутить к защите программ? А очень просто J.
Как вы уже догадались - Сеть Петри является идеальным инструментом для моделирования переходов при выполнении определенных условий.
Не секрет, что большинство защит сводится к максимальному сокрытию и недопущения длинных рук кракера к пресловутому условному переходу (да-да, того самого badguy/goodguyjump). При этом обертка может состоять из самых изощренных анти-отладочных приемов, программа может быть запакована множеством упаковщиков, и любой другой хренью, которую вы только можете себе представить – в середине всей этой мишуры находится один единственный переход (нет, проверок может быть очень много, однако сути дела это не меняет). Итак, рассмотрим простейший пример, на котором можно наглядно просмотреть идею защиты:
Построим простейшую сеть Петри:
Допустим, что при начальной маркировке можно задавать кол-во фишек только в позициях p0…p3. (обратите внимание, что позиция p7 изначально содержит одну фишку). Остальные позиции недоступны для маркирования. Зададим ключевому переходу t2 наименьший приоритет (это означает, что если одновременно разрешены переходы t2 и t1, то сработает переход t1), после чего он (переход t2) выполниться тогда и только тогда, когда начальная маркировка помечает позиции p0…p3 следующим образом: p0=1, p1=0, p2=1, p3=1. При всех остальных допустимых начальных маркировках переход t2 не сработает. Если не верите то попытайтесь на практике опровергнуть это утверждение, но уверяю вас – ничего не выйдет.
Теперь представим, что каждый переход – это поток, который проверяет определенный набор бит на ВХОДЕ (входные позиции) и в зависимости от результата устанавливает биты на ВЫХОДЕ. Так, поток t3 проверяет фишки (биты) в позиции p0 и в зависимости от того есть там фишки (бит установлен) или нет (бит сброшен) устанавливает биты на выходных позициях (p5 и p6).
Допустим, пользователю необходимо зарегистрировать программу, введя 4-битный ключ. Биты ключа (фишки) помещаются в позиции p0,p1,p2 и p3 (если бит установлен, то фишка помещается, нет – значит соотв. позиция остается пустой). Этим обеспечивается начальная маркировка сети.
Программа будет считаться зарегистрированной, если переход t2 сработает (т.е. будет активным). Как уже было показано выше – переход t2 сработает только при такой начальной маркировке: p0=1, p1=0, p2=1, p3=1.
Все это легко можно реализовать программно (см. приложение).
Задача достижимости – основная задача, решаемая при анализе сетей Петри, к которой сводится множество других задач (в частности – задача активности). Задача достижимости формулируется следующим образом: для данной сети Петри С с маркировкой m и маркировки m’ определить: m’ÎR(C,m). Задача активности и достижимости в общем случае не решены.
Дж. Питерсон: стр. 103 «4.2.1.4 Ограниченность дерева достижимости»
«Как видим, дерево достижимости можно использовать для решения задач безопасности, ограниченности, сохранения и покрываемости. К сожалению, в общем случае его нельзя использовать для решения задач достижимости и активности […]»
Решая задачу достижимости с использованием дерева достижимости мы фактически прибегаем к методу полного перебора. К данному методу вообще можно свести любую задачу. Поэтому защищенность здесь определяется только временем и ресурсами, затраченными на полный перебор.
На нашем примере легко видеть, что найти правильный ключ (т.е. правильную начальную маркировку) можно перебрав всего лишь 2^4 = 16 значений. Это можно сделать даже вручную, а взглянув на представление программы в виде сети Петри можно догадаться интуитивно за несколько секунд.
Использование ключей длиной менее 2^128 бит на сегодняшний день не может обеспечить защиту на приличном уровне, именно поэтому предложенная в примере сеть Петри не годится для практической защиты и приведена лишь в качестве наглядной иллюстрации.
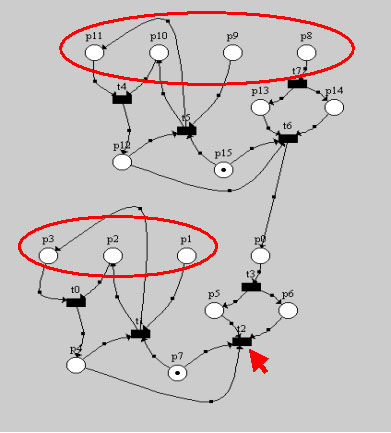
Однако приведенную в примере сеть можно легко «наращивать» автоматически, тем самым усложняя ее структуру и увеличивая длину ключа, что является, возможно, очень важным ее свойством. Под «наращиванием» я понимаю следующее: к каждой позиции, которую можно пометить при начальной маркировке, “подводиться” новая сеть. При этом она теряет возможность быть помеченной при начальной маркировке, однако появляются новые N позиций, которые доступны для начальной маркировки. Например, нарастим сеть над позицией p0. Для этого достаточно просто скопировать уже имеющуюся сеть:
При этом переход t2 остается ключевым и появляются новые позиции (p8…p11), которые можно пометить при начальной маркировке (фактически позиции p8…p11 дублируют смысловое значение позиций p0…p3 в нижней сети).
Легко видеть, что переход t6 фактически выполняет ту же роль, что и переход t2 в «нижней» сети. Очевидно, что для срабатывания перехода t2 необходимо срабатывание перехода t6, а для этого начальной маркировкой необходимо пометить позиции следующим образом:
p1=0, p2=1, p3=1, p8=1, p9=0, p10=1, p11=1.
Длина ключа увеличилась до 2^7 бит. Теперь для полного перебора необходимо осуществить уже 128 проверок.
Надстроив сеть аналогичным образом над p1, p2 и p3 мы получим ключ длиной 16 бит, для полного перебора необходимо рассмотреть 2^16 комбинаций, чего также не достаточно. Продолжая наращивание дальше мы дойдем до 2^128 ключей, что можно считать достаточным для надежной защиты. В идеале размер ключа следует довести до 2^512.
Для простоты остановимся на 16 битном ключе.
Единственная позиция, которая не поддается наращению по аналогии с другими позициями – позиция p1, т.к. для достижимости t2 нам необходимо ее нулевое значение. Если нарастить над ней копию уже имеющейся сети то ее нулевое значение достижимо при 15 (16-1) различных комбинаций. Это означает, что диапазон возможных ключей сужается. Поэтому для перехода p1 следует изменить надстроечную сеть. Одним из вариантов может явиться следующее наращение:
Здесь для того, чтобы переход t11 НЕ СРАБОТАЛ (а это именно то чего нам нужно добиться) начальной маркировкой нужно задать следующие значения:
P16=1, P17=1, P18=0, p19=1
Переходу t11 необходимо задать наименьший приоритет.
Для 16-битного ключа можно построить таблицы переходов (см. приложение “а”).
Важным свойством таблицы переходов является то, что строки (столбцы) таблицы можно переставлять в произвольном порядке, структура сети от этого не меняется, а анализ усложняется.
стр. 145 «5.6. Сложность задачи достижимости»
«Поскольку задачи подмножества и равенства для множеств достижимости сетей Петри неразрешимы, то возможно, что неразрешима также и сама задача достижимости. Однако в настоящее время вопрос, разрешима ли (или неразрешима) задача достижимости, открыт. На сегодняшний день не существует ни алгоритма, решающего задачу достижимости, ни доказательства того, что такого алгоритма не может быть. […]». И это просто замечательно! (по крайней мере для нашей защитной системы). Именно на этом принципе она и строится.
Взлом программ, защищенных с помощью сетей Петри
Напоследок несколько слов о взломе такой защиты. Очевидно, что стандартные методы здесь не подходят. В отличие от программ, защищенных «последовательными» методами, кракер никогда не сможет определить какой из переходов в защите является ключевым, т.к. при неправильной начальной маркировке ключевой переход просто недостижим. С другой стороны, кракер может попытаться запустить все переходы в сети, каким-либо образом обнаружив все позиции. Действительно, для нашего случая с 16-битным ключом ему достаточно перепробовать 20 переходов, вместо 2^16 ключей (т.е. заполнить фишками ВСЕ позиции). Для противостояния данному способу взлома можно пойти несколькими путями:
1. Построить сеть таким образом, чтобы ключевой переход имел наименьший приоритет у окружающих его переходов. То есть один из окружающих переходов сработает раньше и уведет фишку из ключевой позиции, таким образом ключевой переход не сработает.
2. Добавление в сеть такого количества позиций, что полный перебор всех переходов сопоставим с полным перебором всех начальных маркировок. Это единственный способ обеспечить защиту, которая зависит только от длины ключа. Данный метод неэкономичен с точки зрения расхода памяти и скорости обработки.
Надо также заметить, что отладка программы существенно осложняется тем, что для анализа поведения сети необходимо отлаживать одновременно N потоков, где N – кол-во переходов в сети, поэтому взлом программы, защищенной моим методом, может быть осуществлен только статическим эвристическим путем, что при наличии тысяч переходов просто нереально осуществить.
В заключении хочется привести одну мысль, которую следует положить в основу любой защитной системы: главная цель любой защитной системы – скрыть некоторую информацию от кракера. В то же время, любая система защиты искусственна, то есть создана человеком. Любой человек, даже если он непревзойденный гений, способен создать лишь временно устойчивую к атаке защиту, то есть ни одна система защиты не достигает своей единственной и главной цели, откуда, очевидно, следует, что создание защитных систем любого вида занятие бесполезное и бесперспективное.
Однако, наверно, это не совсем так – по крайней мере это очень увлекательно.
Аттач. © Broken Sword
Защита программ с помощью сетей Петри
Дата публикации 18 май 2004