Идентификация SWITCH - CASE - BREAK — Архив WASM.RU
"…когда вы видите все целиком, то у вас нет выбора, вам не из чего
выбирать. Тогда вы имеете два пути одновременно, следуете
одновременно этим двум направлениям"
Ошо "Пустая лодка" Беседы по высказываниям Чжуан Цзы
Для улучшения читабельности программ в язык Си был введен оператор множественного выбора – switch. В Паскале с той же самой задачей справляется оператор CASE, кстати, более гибкий, чем его Си-аналог, но об их различиях мы поговорим попозже.
Легко показать, что switch эквивалентен конструкции "IF (a == x1) THEN оператор1 ELSE IF (a == x2) THEN оператор2 IF (a == x2) THEN оператор2 IF (a == x2) THEN оператор2 ELSE …. оператор по умолчанию". Если изобразить это ветвление в виде логического дерева, то образуется характерная "косичка", прозванная так за сходство с завитой в косу прядью волос – см. рис. 29
Казалось бы, идентифицировать switch никакого труда не составит, – даже не стоя дерева, невозможно не обратить внимания на длинную цепочку гнезд, проверяющих истинность условия равенства некоторой переменной с серией непосредственных значений (сравнения переменной с другой переменной switch не допускает).
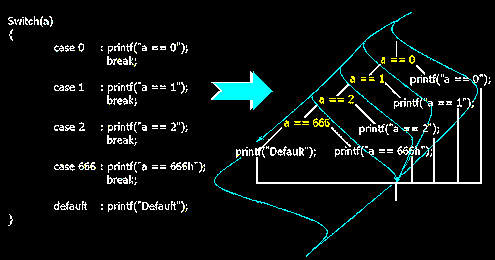
Рисунок 29 0х01С Трансляция оператора switch в общем случае
Однако в реальной жизни все происходит совсем не так. Компиляторы (даже не оптимизирующие) транслируют switch в настоящий "мясной рулет", доверху нашпигованных всевозможными операциями отношений. Давайте, откомпилируем приведенный выше пример компилятором Microsoft Visual C++ и посмотрим, что из этого выйдет:
main proc near ; CODE XREF: start+AF p var_tmp = dword ptr -8 var_a = dword ptr –4 push ebp mov ebp, esp ; Открываем кадр стека sub esp, 8 ; Резервируем место для локальных переменных mov eax, [ebp+var_a] ; Загружаем в EAX значение переменной var_a mov [ebp+var_tmp], eax ; Обратите внимание – switch создает собственную временную переменную! ; Даже если значение сравниваемой переменной в каком-то ответвлении CASE ; будет изменено, это не повлияет на результат выборов! ; В дальнейшем во избежании путаницы, мы будем условно называть ; переменную var_tmp переменной var_a cmp [ebp+var_tmp], 2 ; Сравниваем значение переменной var_a с двойкой ; Хм-хм, в исходном коде CASE начинался с нуля, а заканчивался 0x666 ; Причем же тут двойка?! jg short loc_401026 ; Переход, если var_a > 2 ; Обратите на этот момент особое внимание – ведь в исходном тексте такой ; операции отношения не было! ; Причем, этот переход не ведет к вызову функции printf, т.е. этот фрагмент ; кода получен не прямой трансляцией некой ветки case, а как-то иначе! cmp [ebp+var_tmp], 2 ; Сравниваем значение var_a с двойкой ; Очевидный "прокол" компилятора – мы же только что проделывали эту ; операции, и с того момента не меняли никакие флаги! jz short loc_40104F ; Переход к вызову printf("a == 2"), если var_a == 2 ; ОК, этот код явно получен трансляцией ветки CASE 2: printf("a == 2") cmp [ebp+var_tmp], 0 ; Сравниваем var_a с нулем jz short loc_401031 ; Переход к вызову printf("a == 0"), если var_a == 0 ; Этот код получен трансляцией ветки CASE 0: printf("a == 0") cmp [ebp+var_tmp], 1 ; Сравниваем var_a с единицей jz short loc_401040 ; Переход к вызову printf("a == 1"), если var_a == 1 ; Этот код получен трансляцией ветки CASE 1: printf("a == 1") jmp short loc_40106D ; Переход к вызову printf("Default") ; Этот код получен трансляцией ветки Default: printf("a == 0") loc_401026: ; CODE XREF: main+10 j ; Эта ветка получает управление, если var_a > 2 cmp [ebp+var_tmp], 666h ; Сравниваем var_a со значением 0x666 jz short loc_40105E ; Переход к вызову printf("a == 666h"), если var_a == 0x666 ; Этот код получен трансляцией ветки CASE 0x666: printf("a == 666h") jmp short loc_40106D ; Переход к вызову printf("Default") ; Этот код получен трансляцией ветки Default: printf("a == 0") loc_401031: ; CODE XREF: main+1C j ; // printf("A == 0") push offset aA0 ; "A == 0" call _printf add esp, 4 jmp short loc_40107A ; ^^^^^^^^^^^^^^^^^^^^^^ - а вот это оператор break, выносящий управление ; за пределы switch – если бы его не было, то начали бы выполняться все ; остальные ветки CASE, не зависимо от того, к какому значению var_a они ; принадлежат! loc_401040: ; CODE XREF: main+22 j ; // printf("A == 1") push offset aA1 ; "A == 1" call _printf add esp, 4 jmp short loc_40107A ; ^ break loc_40104F: ; CODE XREF: main+16 j ; // printf("A == 2") push offset aA2 ; "A == 2" call _printf add esp, 4 jmp short loc_40107A ; ^ break loc_40105E: ; CODE XREF: main+2D j ; // printf("A == 666h") push offset aA666h ; "A == 666h" call _printf add esp, 4 jmp short loc_40107A ; ^ break loc_40106D: ; CODE XREF: main+24 j main+2F j ; // printf("Default") push offset aDefault ; "Default" call _printf add esp, 4 loc_40107A: ; CODE XREF: main+3E j main+4D j ... ; // КОНЕЦ SWITCH mov esp, ebp pop ebp ; Закрываем кадр стека retn main endp
Листинг 173Построив логическое дерево (см. "Идентификация IF – THEN – ELSE"), мы получим следующую картину (см. рис. 30). При ее изучении бросается в глаза, во-первых, условие "a >2", которого не было в исходной программе, а во-вторых, изменение порядка обработки case. В то же время, вызовы функций printf следуют один за другим строго согласно их объявлению. Зачем же компилятор так чудит? Чего он рассчитывает этим добиться?
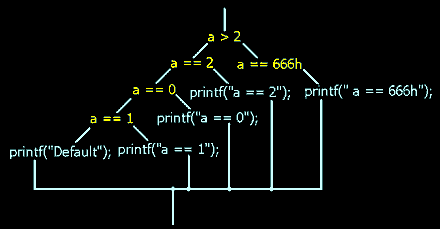
Рисунок 30 0x01D Пример трансляция оператора switch компилятором Microsoft Visual C
Назначение гнезда (a > 2) объясняется очень просто – последовательная обработка всех операторов case крайне непроизводительная. Хорошо, если их всего четыре-пять штук, а если программист натолкает в switch сотню - другую case? Процессор совсем запарится, пока их все проверит (а по закону бутерброда нужный case будет в самом конце). Вот компилятор и "утрамбовывает" дерево, уменьшая его высоту. Вместо одной ветви, изображенной на рис. 30, транслятор в нашем случае построил две, поместив в левую только числа не большие двух, а в правую – все остальные. Благодаря этому, ветвь "666h" из конца дерева была перенесена в его начало. Данный метод оптимизации поиска значений называют "методом вилки", но не будет сейчас на нем останавливаться, а лучше разберем его в главе "Обрезка длинных деревьев".
Изменение порядка сравнений – право компилятора. Стандарт ничего об этот не говорит и каждая реализация вольна поступать так, как ей это заблагорассудится. Другое дело – case-обработчики (т.е. тот код, которому case передает управление в случае истинности отношения). Они обязаны располагаться так, как были объявлены в программе, т.к. при отсутствии закрывающего оператора break они должны выполняться строго в порядке, замышленном программистом, хотя эта возможность языка Си используется крайне редко.
Таким образом, идентификация оператора switch не сильно усложняется: если после уничтожения узлового гнезда и прививки правой ветки к левой (или наоборот) мы получаем эквивалентное дерево, и это дерево образует характерную "косичку" – мы имеем дело с оператором множественного выбора или его аналогом.
Весь вопрос в том: правомерны ли мы удалять гнездо, не нарушит ли эта операция структуры дерева? Смотрим – на левой ветке узлового гнезда расположены гнезда (a == 2), (a == 0) и (a == 1), а на левом – (a==0x666) Очевидно, если a == 0x666, то a != 0 и a != 1! Следовательно, прививка правой ветки к левой вполне безопасна и после такого преобразования дерево принимает вид типичный для конструкции switch (см. рис. 31)

Рисунок 31 0x01E Усечение логического дерева
Увы, такой простой прием идентификации срабатывает не всегда! Иные компиляторы такого наворотят, что волосы в разных местах дыбом встанут! Если откомпилировать наш пример компилятором Borland C++ 5.0, то код будет выглядеть так:
; int __cdecl main(int argc,const char **argv,const char *envp) _main proc near ; DATA XREF: DATA:00407044 o push ebp mov ebp, esp ; Открываем кадр стека ; Компилятор помещает нашу переменную a в регистр EAX ; Поскольку она не была инициализирована, то заметить этот факт ; не так-то легко! sub eax, 1 ; Уменьшает EAX на единицу! Что бы этого значило, хвост Тиггера? ; Никакого вычитания в нашей программе не было! jb short loc_401092 ; Если EAX < 1, то переход на вызов printf("a == 0") ; (мы ведь помним, что CMP та же команда SUB, только не изменяющая операндов?) ; Ага, значит, этот код сгенерирован в результате трансляции ; ветки CASE 0: printf("a == 0"); ; Внимание! задумайтесь: какие значения может принимать EAX, чтобы ; удовлетворять условию этого отношения? На первый взгляд, EAX < 1, ; в частости, 0, -1, -2,… СТОП! Ведь jb - это беззнаковая инструкция ; сравнения! А -0x1 в беззнаковом виде выглядит как 0xFFFFFFFF ; 0xFFFFFFFF много больше единицы, следовательно, единственным подходящим ; значением будет ноль ; Таким образом, данная конструкция - просто завуалированная проверка EAX на ; равенство нулю! (Ох! и хитрый же этот Borland - компилятор!) ; jz short loc_40109F ; Переход, если установлен флаг нуля ; Он будет он установлен в том случае, если EAX == 1 ; И действительно переход идет на вызов printf("a == 1") dec eax ; Уменьшаем EAX на единицу jz short loc_4010AC ; Переход если установлен флаг нуля, а он будет установлен когда после ; вычитания единицы командой SUB, в EAX останется ровно единица, ; т.е. исходное значение EAX должно быть равно двум ; И точно - управление передается ветке вызова printf("a == 2")! sub eax, 664h ; Отнимаем от EAX число 0x664 jz short loc_4010B9 ; Переход, если установлен флаг нуля, т.е. после двукратного уменьшения EAX ; равен 0x664, следовательно, исходное значение - 0x666 jmp short loc_4010C6 ; прыгаем на вызов printf("Default"). Значит, это - конец switch loc_401092: ; CODE XREF: _main+6 j ; // printf("a==0"); push offset aA0 ; "a == 0" call _printf pop ecx jmp short loc_4010D1 loc_40109F: ; CODE XREF: _main+8 j ; // printf("a==1"); push offset aA1 ; "a == 1" call _printf pop ecx jmp short loc_4010D1 loc_4010AC: ; CODE XREF: _main+B j ; // printf("a==2"); push offset aA2 ; "a == 2" call _printf pop ecx jmp short loc_4010D1 loc_4010B9: ; CODE XREF: _main+12 j ; // printf("a==666"); push offset aA666h ; "a == 666h" call _printf pop ecx jmp short loc_4010D1 loc_4010C6: ; CODE XREF: _main+14 j ; // printf("Default"); push offset aDefault ; "Default" call _printf pop ecx loc_4010D1: ; CODE XREF: _main+21 j _main+2E j ... xor eax, eax pop ebp retn _main endp
Листинг 174Код, сгенерированный компилятором, модифицирует сравниваемую переменную в процессе сравнения! Оптимизатор посчитал, что DEC EAX короче, чем сравнение с константой, да и работает шустрее. Вот только нам, хакером, от этого утешения ничуть не легче! Ведь прямая ретрансляция кода (см. "Идентификация IF - THEN - ELSE") дает конструкцию вроде: "if (a-- == 0) printf("a == 0"); else if (a==0) printf("a == 1"); else if (--a == 0) printf("a == 2"); else if ((a-=0x664)==0) printf("a == 666h); else printf("Default")", - в которой совсем не угадывается оператор switch! Впрочем, почему это "не угадывается"?! Угадывается, еще как! Где есть длинная цепочка "IF-THEN-ELSE-IF-THEN-ELSE…" там и до switch-а недалеко! Узнать оператор множественного выбора будет еще легче, если изобразить его в виде дерева - смотрите (см. рис. 32) вот она, характерная "косичка"!
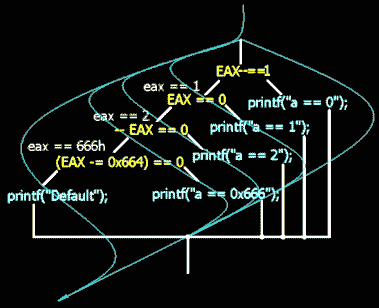
Рисунок 32 0x01F Построение логического дерева с гнездами, модифицирующими саму сравниваемую переменную
Другая характерная деталь - case-обработчики, точнее оператор break традиционно замыкающий каждый из них. Они-то и образуют правую половину "косички", сходясь все вместе с точке "Z". Правда, многие программисты питают паралогическую любовь к case-обработчикам размером в два-три экрана, включая в них помимо всего прочего и циклы (о них речь еще впереди - см. "Идентификация for\while"), и ветвления, и даже вложенные операторы множественно выбора! В результате правая часть "косички" превращается в непроходимый таежный лес, сквозь который не проберется и стадо слонопотамов. Но даже если и так - левая часть "косички", все равно останется достаточно простой и легко распознаваемой!
В заключение темы рассмотрим последний компилятор - WATCOM C. Как и следует ожидать, здесь нас подстерегают свои тонкости и "вкусности". Итак, откомпилированный им код предыдущего примера должен выглядеть так:
main_ proc near ; CODE XREF: __CMain+40 p push 8 call __CHK ; Проверка стека на переполнение cmp eax, 1 ; Сравнение регистровой переменной EAX, содержащей в себе переменную a ; со значением 1 jb short loc_41002F ; Если EAX == 0, то переход к ветви с дополнительными проверками jbe short loc_41003A ; Если EAX == 1 (т.е. условие bellow уже обработано выше), то переход ; к ветке вызова printf("a == 1"); cmp eax, 2 ; Сравнение EAX со значением 2 jbe short loc_410041 ; Если EAX == 2 (условие EAX <2 уже было обработано выше), то переход ; к ветке вызова printf("a == 2"); cmp eax, 666h ; Сравнение EAX со значением 0x666 jz short loc_410048 ; Если EAX == 0x666, то переход к ветке вызова printf("a == 666h"); jmp short loc_41004F ; Что ж, ни одно из условий не подошло - переходит к ветке "Default" loc_41002F: ; CODE XREF: main_+D j ; // printf("a == 0"); test eax, eax jnz short loc_41004F ; Совершенно непонятно - зачем здесь дополнительная проверка?! ; Это ляп компилятора - она ни к чему! push offset aA0 ; "A == 0" ; Обратите внимание - WATCOM сумел обойтись всего одним вызовом printf! ; Обработчики case всего лишь передают ей нужный аргумент! ; Вот это действительно - оптимизация! jmp short loc_410054 loc_41003A: ; CODE XREF: main_+F j ; // printf("a == 1"); push offset aA1 ; "A == 1" jmp short loc_410054 loc_410041: ; CODE XREF: main_+14 j ; // printf("a == 2"); push offset aA2 ; "A == 2" jmp short loc_410054 loc_410048: ; CODE XREF: main_+1B j ; // printf("a == 666h"); push offset aA666h ; "A == 666h" jmp short loc_410054 loc_41004F: ; CODE XREF: main_+1D j main_+21 j ; // printf("Default"); push offset aDefault ; "Default" loc_410054: ; CODE XREF: main_+28 j main_+2F j ... call printf_ ; А вот он наш printf, получающий аргументы из case-обработчиков! add esp, 4 ; Закрытие кадра стека retn main_ endp
Листинг 175В общем, WATCOM генерирует более хитрый, но, как ни странно, весьма наглядный и читабельный код.
::Отличия switch от оператора case языка Pascal. Оператор CASE языка Pascal практически идентичен своему Си собрату - оператору switch, хотя и близнецами их не назовешь: оператор CASE выгодно отличается поддержкой наборов и диапазонов значений. Ну, если обработку наборов можно реализовать и посредством switch, правда не так элегантно как на Pascal (см. листинг 176), то проверка вхождения значения в диапазон на Си организуется исключительно с помощью конструкции "IF-THEN-ELSE". Зато в Паскале каждый case-обработчик принудительно завершается неявным break, а Си-программист волен ставить (или не ставить) его по своему усмотрению.
CASE a OF switch(a) begin { 1 : WriteLn('a == 1'); case 1 : printf("a == 1"); break; 2,4,7 : WriteLn('a == 2|4|7'); case 2 : case 4 : case 7 : printf("a == 2|4|7"); break; 9 : WriteLn('a == 9'); case 9 : printf("a == 9"); break; end;
Листинг 176Однако оба языка накладывают жесткое ограничение на выбор сравниваемой переменной: она должна принадлежать к перечисленному типу, а все наборы (диапазоны) значений представлять собой константы или константные выражения, вычисляемые на стадии компиляции. Подстановка переменных или вызовов функций не допускается.
Представляет интерес посмотреть: как Pascal транслирует проверку диапазонов и сравнить его с компиляторами Си. Рассмотрим следующий пример:
VAR a : LongInt; BEGIN CASE a OF 2 : WriteLn('a == 2'); 4, 6 : WriteLn('a == 4 | 6 '); 10..100 : WriteLn('a == [10,100]'); END; END.
Листинг 177Результат его компиляции компилятором Free Pascal должен выглядеть так (для экономии места приведена лишь левая часть "косички"):
mov eax, ds:_A ; Загружаем в EAX значение сравниваемой переменной cmp eax, 2 ; Сравниваем EAX со значением 0х2 jl loc_CA ; Конец CASE ; Если EAX < 2, то - конец CASE sub eax, 2 ; Вычитаем из EAX значение 0x2 jz loc_9E ; WriteLn('a == 2'); ; Переход на вызов WriteLn('a == 2') если EAX == 2 sub eax, 2 ; Вычитаем из EAX значение 0x2 jz short loc_72 ; WriteLn('a == 4 | 6'); ; Переход на вызов WriteLn(''a == 4 | 6') если EAX == 2 (соотв. a == 4) sub eax, 2 ; Вычитаем из EAX значение 0x2 jz short loc_72 ; WriteLn('a == 4 | 6'); ; Переход на вызов WriteLn(''a == 4 | 6') если EAX == 2 (соотв. a == 6) sub eax, 4 ; Вычитаем из EAX значение 0x4 jl loc_CA ; Конец CASE ; Переход на конец CASE, если EAX < 4 (соотв. a < 10) sub eax, 90 ; Вычитаем из EAX значение 90 jle short loc_46 ; WriteLn('a = [10..100]'); ; Переход на вызов WriteLn('a = [10..100]') если EAX <= 90 (соотв. a <= 100) ; Поскольку, случай a > 10 уже был обработан выше, то данная ветка ; срабатывает при условии a>=10 && a<=100. jmp loc_CA ; Конец CASE ; Прыжок на конец CASE - ни одно из условий не подошло
Листинг 178Как видно, Free Pascal генерирует практически тот же самый код, что и компилятор Borland C++ 5.х, поэтому его анализ не должен вызвать никаких сложностей.
__::IDA распознает switch
::Обрезка (балансировка) длинных деревьев. В некоторых (хотя и редких) случаях, операторы множественного выбора содержат сотни (а то и тысячи) наборов значений, и если решать задачу сравнения "в лоб", то высота логического дерева окажется гигантской до неприличия, а его прохождение займет весьма длительное время, что не лучшим образом скажется на производительности программы.
Но, задумайтесь: чем собственно занимается оператор switch? Если отвлечься от устоявшейся идиомы "оператор SWITCH дает специальный способ выбора одного из многих вариантов, который заключается в проверке совпадения значения данного выражения с одной из заданных констант и соответствующем ветвлении", то можно сказать, что switch - оператор поиска соответствующего значения. В таком случае каноническое switch - дерево представляет собой тривиальный алгоритм последовательного поиска - самый неэффективный алгоритм из всех.
Пусть, например, исходный текст программы выглядел так:
. switch (a) { case 98 : …; case 4 : …; case 3 : …; case 9 : …; case 22 : …; case 0 : …; case 11 : …; case 666: …; case 096: …; case 777: …; case 7 : …; }
Листинг 179Тогда соответствующее ему не оптимизированное логическое дерево будет достигать в высоту одиннадцати гнезд (см. рис. 33 слева). Причем, на левой ветке корневого гнезда окажется аж десять других гнезд, а на правой - вообще ни одного (только соответствующий ему case - обработчик).
Исправить "перекос" можно разрезав одну ветку на две и привив образовавшиеся половинки к новому гнезду, содержащему условие, определяющее в какой из веток следует искать сравниваемую переменную. Например, левая ветка может содержать гнезда с четными значениями, а правая - с нечетными. Но это плохой критерий: четных и нечетных значений редко бывает поровну и вновь образуется перекос. Гораздо надежнее поступить так: берем наименьшее из всех значений и бросаем его в кучу А, затем берем наибольшее из всех значений и бросаем его в кучу B. Так повторяем до тех пор, пока не рассортируем все, имеющиеся значения.
Поскольку оператор множественного выбора требует уникальности каждого значения, т.е. каждое число может встречаться в наборе (диапазоне) значений лишь однажды, легко показать, что: а) в обеих кучах будет содержаться равное количество чисел (в худшем случае - в одной куче окажется на число больше); б) все числа кучи A меньше наименьшего из чисел кучи B. Следовательно, достаточно выполнить только одно сравнение, чтобы определить в какой из двух куч следует искать сравниваемое значения.
Высота нового дерева будет равна ((N+1/2)+1), где N - количество гнезд старого дерева. Действительно, мы же ветвь дерева надвое и добавляем новое гнездо - отсюда и берется N/2 и +1, а (N+1) необходимо для округления результата деления в большую сторону. Т.е. если высота не оптимизированного дерева достигала 100 гнезд, то теперь она уменьшилась до 51. Что? Говорите, 51 все равно много? А что нам мешает разбить каждую из двух ветвей еще на две? Это уменьшит высоту дерева до 27 гнезд! Аналогично, последующее уплотнение даст 16 ' 12 ' 11 ' 9 ' 8… и все! Более плотная упаковка дерева невозможна (подумайте почему - на худой конец постройте само дерево). Но, согласитесь, восемь гнезд - это не сто! Полное прохождение оптимизированного дерева потребует менее девяти сравнений!
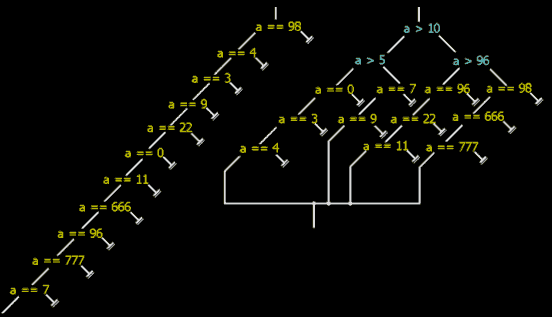
Рисунок 33 0х21 Логическое дерево до утрамбовки (слева) и после (справа)
"Трамбовать" логические деревья оператора множественного выбора умеют практически все компиляторы - даже не оптимизирующие! Это увеличивает производительность, но затрудняет анализ откомпилированной программы. Взгляните еще раз на рис. 33 - левое несбалансированное дерево наглядно и интуитивно - понятно. После же балансировки (правое дерево) в нем Тиггер хвост обломит.
К счастью, балансировка дерева допускает эффективное обращение. Но прежде, чем засучить рукава и приготовиться к лазанью по деревьям (а Тиггеры по деревьям лазают лучше всех!) введем понятие балансировочного узла. Балансировочный узел не изменяет логики работы двоичного дерева и являются факультативным узлов, единственная функция которого укорачивание длины ветвей. Балансировочный узел без потери функциональности дерева может быть замещен любой из своих ветвей. Причем каждая ветвь балансировочного узла должна содержать одно или более гнезд.
Рассуждая от противного - все узлы логического дерева, правая ветка которых содержит одно или более гнезд, могут быть замещены на эту самую правую ветку без потери функциональности дерева, то данная конструкция представляет собой оператор switch. Почему именно правая ветка? Так ведь оператор множественного выбора в "развернутом" состоянии представляет цепочку гнезд, соединенных левыми ветвями друг с другом, а на правых держащих case-обработчики, - вот мы и пытаемся подцепить все правые гнезда на левую ветвь. Если это удается, мы имеем дело с оператором множественного выбора, а нет - с чем-то другим.
Рассмотрим обращение балансировки на примере следующего дерева (см. рис. 34 слева). Двигаясь от левой нижней ветви, мы будем продолжать взбираться на дерево до тех пор, пока не встретим узел, держащий на своей правой ветви одно или более гнезд. В нашем случае - это узел (a > 5). Смотрите: если данный узел заменить его гнездами (a==7) и (a == 9) функциональность дерева не нарушиться! (см. рис. 34 посередине). Аналогично узел (a > 10) может быть безболезненно заменен гнездами (a > 96), (a == 96), (a == 22) и (a == 11), а узел (a > 96) в свою очередь - гнездами (a == 98), (a == 666) и (a == 777). В конце -концов образуется классическое switch-дерево, в котором оператор множественного выбора распознается с первого взгляда.



Рисунок 34 0x22 Обращение балансировки логического дерева
Сложные случаи балансировки или оптимизирующая балансировка. Для уменьшения высоты "утрамбовываемого" дерева хитрый трансляторы стремятся замещать уже существующие гнезда балансировочными узлами. Рассмотрим следующий пример: (см. рис. 35). Для уменьшения высоты дерева транслятор разбивает его на две половины - в левую идут гнезда со значениями меньшие или равные единицы, а в правую - все остальные. Казалось бы, на правой ветке узла (a > 1) должно висеть гнездо (a == 2), ан нет! Здесь мы видим узел (a >2), к левой ветки которого прицеплен case-обработчик :2! А что, вполне логично - если (a > 1) и !(a > 2), то a == 2!
Легко видеть, что узел (a > 2) жестко связан с узлом (a > 1) и работает на пару с последним. Нельзя выкинуть один из них, не нарушив работоспособности другого! Обратить балансировку дерева по описанному выше алгоритму без нарушения его функциональности невозможно! Отсюда может создаться мнение, что мы имеем дело вовсе не с оператором множественного выбора, а чем-то другим.
Чтобы развеять это заблуждение придется предпринять ряд дополнительных шагов. Первое - у switch-дерева все case-обработчики всегда находятся на правой ветви. Смотрим - можно ли трансформировать наше дерево так, чтобы case-обработчик 2 оказался на левой ветви балансировочного узла? Да, можно: заменив (a > 2) на (a < 3) и поменяв ветви местами (другими словами выполнив инверсию). Второе - все гнезда switch-дерева содержат в себе условия равенства, - смотрим: можем ли мы заменить неравенство (a < 3) на аналогичное ему равенство? Ну, конечно же, можем - (a == 2)!
Вот, после всех этих преобразований, обращение балансировки дерева удается выполнить без труда!
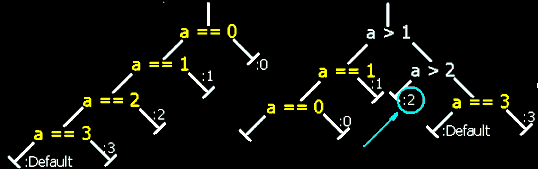
Рисунок 35 0x23 Хитрый случай балансировки
Ветвления в case-обработчиках. В реальной жизни case-обработчики прямо-таки кишат ветвлениями, циклами и прочими условными переходами всех мастей. Как следствие - логическое дерево приобретает вид ничуть не напоминающий оператор множественного выбора, а скорее смахивающий на заросли чертополоха, так любимые И-i. Понятное дело - идентифицировав case-обработчики, мы могли бы решить эту проблему, но как их идентифицировать?!
Очень просто - за редкими клиническими исключениями, case-обработчики не содержат ветвлений относительно сравниваемой переменной. Действительно, конструкции "switch(a) …. case 666 : if (a == 666) …." или "switch(a) …. case 666 : if (a > 66) …." абсолютно лишены смысла. Таким образом, мы можем смело удалить из логического дерева все гнезда с условиями, не касающимися сравниваемой переменной (переменной коневого гнезда).
Хорошо, а если программист в порыве собственной глупости или стремлении затруднить анализ программы "впаяет" в case-обработчики ветвления относительно сравниваемой переменной?! Оказывается, это ничуть не затруднит анализ! "Впаянные" ветвления элементарно распознаются и обрезаются либо как избыточные, либо как никогда не выполняющиеся. Например, если к правой ветке гнезда (a == 3) прицепить гнездо (a > 0) - его можно удалить, как не несущее в себе никакой информации. Если же к правой ветке того же самого гнезда прицепить гнездо (a == 2) его можно удалить, как никогда не выполняющееся - если a == 3, то заведомо a != 2! © Крис Касперски
Идентификация SWITCH - CASE - BREAK
Дата публикации 16 июн 2002
