Введение в крэкинг с нуля, используя OllyDbg - Глава 5 — Архив WASM.RU
МАТЕМАТИЧЕСКИЕ ИНСТРУКЦИИ
INC И DEC
Эти инструкции увеличивают или уменьшают значение операнда, прибавляя к нему один в случае с INC или, соответственно, отнимая один в случае с DEC.
Идём в Олли и, как обычно, открываем крэкми CrueHead'и и в первой строке пишем:

На моей машине EAX изначально равен нулю. Если у вас это не так, вы можете изменить это вручную.

Затем нажимаем F7 и выполняем инструкцию INC EAX, увеличивая его на один.

Таким же образом можем ввести DEC сразу под предыдущей инструкцией.

Нажимаем F7 и выполняем инструкцию INC EAX, которая уменьшает значение регистра на 1, после чего он принимает предыдущее значение - 0.

Также можно увеличивать или уменьшать значение ячейки памяти.

Хотя сейчас ничего не выйдет, так как у секции нет разрешения на запись, поэтому совершить данную операцию нельзя, в связи с чем генерируется исключение.

Что было бы, если бы у секции было выставлено разрешение на запись? Идём в DUMP по адресу 405000.

Содержимое, если его прочитать наоборот, будет равно 00001000, значит, если бы оно было увеличено, то было бы 00001001

В данном случае для DWORD прибавление 1 производилось к 4 байтам содержимого.
Для WORD суммирование будет применено только к двум последним байтам.

И при BYTE суммирование будет применено только к последнему байту.

ADD
ADD, как можно видеть, суммирует оба операнда, сохраняя результат в первом.
ADD EAX, 1 похоже на INC EAX.
Также можем складывать регистры.
Идём в Олли.

До выполнения инструкции:
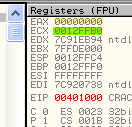
На моейм машине EAX содержит 00000000, а EAX - 12FFB0. У вас данные регистры могут содержать другие значения, также вы можете, если хотите, их изменить, но когда вы нажмёте F7, оба значения будут сложены, а результат помещён в EAX. Смотрим:

Здесь EAX стал красного цвета, потому что он был модифицирован и содержит результат суммирования.
Также можем сложить регистр с содержимым ячейки памяти.

В данном случае нет проблем с правами на запись, так как меняется и сохраняет результат регистр EAX, а содержимое [405000] остаётся неизменным. Соответственно, не генерится и никакого исключения.
До нажания F7 видим, что EAX содержит 0, а по адресу 405000 находится значение 00001000.


Нажимае F7, после чего вычисляется сумма.

Так как EAX = 0, то в EAX сохраняется результат, равный 1000.
Если хотим, чтобы результат сохранился в памяти, то пишем:

В этом случае результат сохранится в 405000, и так как это модифицирует память, то в нашем случае при нажатии на F7 будет сгенерировано исключение об отсутствии прав на запись.

ADC (ADD С ПЕРЕНОСОМ)
В данном случае вычисляется сумма обоих операндов и флага переноса, а конечный результат сохраняется в первом из операндов.


Здесь видим, что здесь будет суммирован EAX, содержащий 21, со числом 3, а также вычислен флаг C, который сейчас равен нулю. Нажимаем F7.

Видим, что результат равен 24. Теперь повторим эту операцию, но с флагом C равным 1, значение которого мы можем изменить, если дважды кликнем по нему мышью.

Сделав это, повторяем выполнение инструкции, изменив значение флага C.

Нажимем F7 и вуаля - результат равен 25.

Так как сумма EDX (21) с 3 и флагом C, равном 1, равна 25.
SUB
Это операция является обратной по отношению к ADD - она вычисляет остаток от вычитания второго операнда от первого и сохраняет в последнем полученный результат.

На моей машине регистры до выполнения инструкции содержали следующее:

По нажатию F7 инструкция вычтет от EAX, который содержит ноль, значение 2.
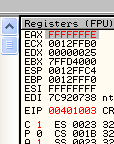
Результатом является -2, что в шестнадцатеричной системе выглядит как FFFFFFFE, в чём мы можем убедиться, если кликнем два раза мышью на данном значении:
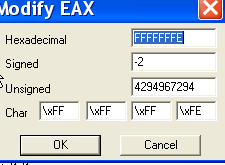
Видим, что в десятеричной системе это равно -2.
Также можно отнимать значение регистров и ячеек памяти примерно таким же образом, как и при использовании инструкции ADD.
Код (Text):
То есть EAX-ECX с сохранением результата в EAX.
И
Код (Text):
Вычитает от EAX содержимое ячейки памяти по адресу 405000, сохраняя результат в EAX.
Обратный случай:
Код (Text):
Так как результата сохраняется .в первый операнд, то, поскольку у нас нет прав на запись в секцию, то получим исключение.
SBB
Это операция является обратной к ADC: она вычисляет разность между операндами, отнимает от того, что получилось, значение флага переноса (флаг C) и сохраняется окончательный результат в первый операнд.

До выполнения в EDX находилось 21, а флаг переноса был равен 0.

Нажатие на F7 вычтет из EDX число 3, а затем ноль, которому равен флаг C.

Теперь повторим операцию, присвоив флагу C значение 1.

Нажимает на F7 и теперь из EDX вычитается 3, а затем единица, которой равен флаг C.

В данном случае результат равен 1D.
MUL
Ок, есть две инструкции для выполнения умножения. Первой из них является MUL, которая не учитывает знаки чисел. Она использует только один операнд, а другим всегда является EAX Результат сохраняется в EDX:EAX.
Например:
Код (Text):
Здесь ECX умножается на EAX без учёта знаков их значений, а результат сохраняется в EDX:EAX.
Рассмотрим следующий пример с помощью OllyDbg:


Поместим в EAX число FFFFFFF7, в ECX - 9, а затем посчитаем результат с помощью стандартного калькулятора Windows:


Получится:

Это не поместится в EAX. Посмотрим, что будет в Олли и нажмём на F7.

EDX и EAX выделены красным, так как их значение было изменено, и, как видим, в EAX было сохранено то, что поместилось, а остальное в EDX. В данном случае 8-рка, которую не смог вместить EAX, попала в EDX, поэтому в таких случая говорят, что результат содержится в EDX:EAX, то есть два регистра используются как один двойного размера.
В случае с
Код (Text):
Происходит умножение ячейки памяти по адресу 405000 на EAX, а результат, как обычно, помещается в EDX:EAX без учёта знаков операндов.
Чтобы посмотреть в Олли как выглядит какое-либо шестнадцатеричное значение без учёта знака, кликните два раза мышью на любом регистре.
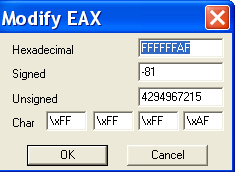
Как можно видеть, во втором ряду находится значение со знаком (в данном случае FFFFFFAF это -81, если учитывать знак), но в таких операциях как MUL все числа считаются БЕЗЗНАКОВЫМИ. Третья строка как раз и содержит десятеричное значение без знака. Сейчас видим, что число FFFFFFAF - это 4294967215, если рассматривать его как положительное, то есть беззнаковое.
IMUL (умножение без знака)
Инструция IMUL - это умножение со знаком и употребляется аналогично MUL.
IMUL ECX
Данная операция производит умножение ECX на EAX, а результат сохраняется в EDX:EAX с учётом знака операндов.
Несмотря на сходство с предыдущей инструкцией, IMUL позволяет использовать больше одного операнда, что невозможно в случае с MUL.
Из туториала CAOS'а:
Несмотря на использовальние регистров EAX и EDX по умолчанию, можно указать другие источники и приёмники данных вплоть до трёх операндов. Первый - место, куда необходимо поместить результат и которое всегда должно быть регистром, второй и третий - два значения, которые нужно перемножить. В этих примерах увидим применение этой инструкции с двумя или тремя операндами.Код (Text):
Это первый пример, который похож на MUL, не считая того, что здесь учитываются знаки.
696E74020080FF imul ebp, dword ptr [esi+74], FF800002 [ESI+74] x FF800002 -> EBP
Это второй пример, в котором три операнда: содержимое ESI+74 умножается на FF800002, а результат сохраняется в EBP. Мы можем посмотреть его в действии с помощью Олли.
Скопируем строку "imul ebp, dword ptr [esi+74], FF800002" в Олли.

Видим, что нажатие кнопки "ASSEMBLE" выдаёт ошибку. Это происходит из-за того, что в Олли к числам, которые начинаются с букв, нужно слева приписывать ноль. Исправляем:

Теперь нажатие на ASSEMBLE проходит без ошибок.

Изменяем значение ESI на 401000, чтобы быть уверенными, что адрес ESI + 74, из котого будет происходить чтение, существует.

Видим в пояснениях:
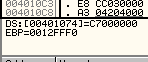
Здесь говорится, что ESI + 74 - это адрес 401074, содержимым которого является C7000000. Идём в DUMP с помощью "GOTO EXPRESSION 401074".

Это значение, которое, если прочитать его наоборот, равно C7000000, будет умножено на FF800002, а результат данной операции будет сохранён в EBP.
Код (Text):
Нажав F7, видим, что EBP стал красным, так как сейчас он содержит результат.

Калькулятор даёт нам следующий результат операции C7000000 * FF800002:

Но поскольку EBP не может вместить его полностью, то в нём остаётся только то, что поместилось, а остальное отбрасывается.
В третьем примере только два операнда, оба из которых перемножаются, а результат сохраняется в первый из них.
Код (Text):
Как видим, основной способ для умножения больших чисел - использовать IMUL только с одним операндом, так как в этом случае результат сохраняется в EDX:EAX, то есть он может быть двойного размера, чего нельзя добиться при использовании двух или трёх операндах, соответственно, данную возможность следует применять для маленьких чисел.
DIV (Unsigned Divide) / IDIV (Signed Divide)
Это инструкции, обратные по отношении к MUL и IMUL соответственно.
DIV имеет только один операнд, не учитывает знаки и сохраняет результат в EDX:EAX.
IDIV всегда учитывает знаки. Если используется один операнд, то, как и DIV, сохраняет результат в EDX:EAX, в случае двух - делит один на другой и сохраняет результат в первый, а при трёх операндах делит второй на третий и сохраняет то, что получилось, в первый.
Не думаю, что нужно приводить здесь примеры, похожие на те, что были в разделе, посвящённом MUL и IMUL.
XADD (Обменять и сложить)
Как можно догадаться, это смесь XCHG и ADD, то есть если :
Код (Text):

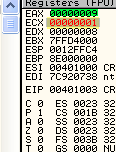
Видим, что ECX равен 1, а EAX - 9. По нажатию на F7 они обменяются значениям, т.е. в EAX попадёт 1, а в ECX - 9, после чего произойдёт сложение.

Видно, что результат затем был сохранён в первый операнд. Регистр ECX содержит число 9, которое находилось до выполнения операции в EAX.
NEG
Назначением данной инструкции является менять знак заданного числа на противоположный, т.е. если у нас есть число 32 в шестнадцатеричной системе, и мы применяем к ней NEG, то результатом будет его отрицательный аналог.
Пример:

Пишем в Олли NEG EAX и заносим в EAX число 32.
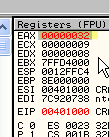
После нажатия на F7 в EAX окажется отрицательный вариант числа 32. Смотрим:
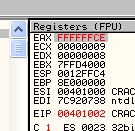

Во втором ряду видим, что результатом является -50 в десятеричной системе (это соответствует -32 в шестнадцатеричной).

Если напечатаем в CommandBar'е число -32 в шестнадцатеричной системе, чтобы выяснить, чему оно равно в десятеричной, то получим ответ, что это значение эквивалентно -50, а также пояснение, что это FFFFFFCE.
Так что видим, что NEG меняет знак операнда на обратный.
ЛОГИЧЕСКИЕ ИНСТРУКЦИИ
Далее следуют логические инструкции, принимающие по два операнда, производящие над ними побитовые операции и сохраняющие результат в первый операнд.
AND
Результатом этой операции над двумя битам является 1, если они оба равны 1, и 0 во всех остальных случаях.
Посмотрим пример в OllyDbg:
- 1 and 1 = 1
- 1 and 0 = 0
- 0 and 1 = 0
- 0 and 0 = 0
Код (Text):

Делаем ECX=00001200, а EAX=3500.

Чтобы сделать эту операцию вручную, нужно перевести оба числа в двоичный вид:
- 1200 в двоичном виде будет равно 01001000000000
- 3500 в двоичном виде будет равно 11010100000000
Применим вышеприведённую таблицу операции AND побитно, например, к последней цифре:

Из двух нулей получится ноль. Повторим эту процедуру над всеми битами и получим 01000000000000, поскольку ситуация, когда оба биты равны 1 у нас встречается только один раз, а посему и в результате единица встретится тоже только один раз.

Если нажмём F7 в Олли, то увидим, что в ECX находится результат 1000, что эквивалентно 01000000000000 в двоичном виде.

OR
В этой инструкции используется примерно тот же метод, что и в предыдущем, за исключением того, что используется другая таблица.
Получается 1, если один или оба бита равны 1, и 0 во всех остальных случаях.
- 1 or 1 = 1
- 1 or 0 = 1
- 0 or 1 = 1
- 0 or 0 = 0
XOR
Здесь то же самое, только используем таблицу функции XOR.
Получается 1, если один и только один из двух битов равен 1, и 0 во всех остальных случаях.
- 1 xor 1 = 0
- 1 xor 0 = 1
- 0 xor 1 = 1
- 0 xor 0 = 0
NOT
Просто инвертирует значение:
- not 1 = 0
- not 0 = 1
Пример: not 0110 = 1001
Если у нас, например, EAX=1200, что в двоичном виде равно 1001000000000, то все нули превратятся в 1, а все 1 в 0.
Код (Text):
После применения NOT получим
Код (Text):
что в калькуляторе Windows в шестнадцатеричном виде отобразится как FFFFEDFF.
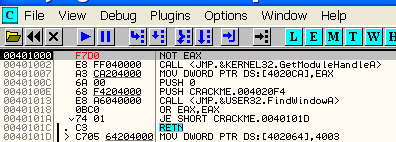
В Олли до нажатия на F7 сделаем EAX равным 1200.

Нажимаем F7.

Видим, что результат тот же самый.
Ок, здесь мы закончим пятую часть "Введения...". Пока подумайте над тем, что узнали в этой главе, а нам ещё предстоит рассмотреть инструкции сравнения, выходов, call и ret.
Шаг за шагом дорога приведёт нас к цели.
© Рикардо Нарваха, пер. Aquila
Введение в крэкинг с нуля, используя OllyDbg - Глава 5
Дата публикации 31 янв 2007
